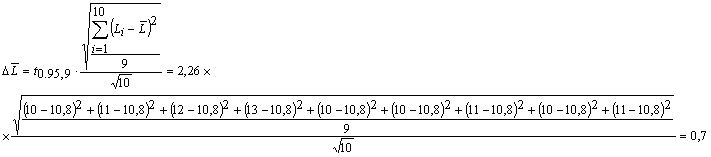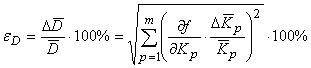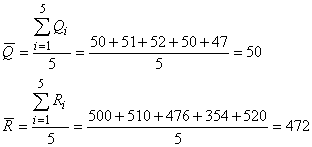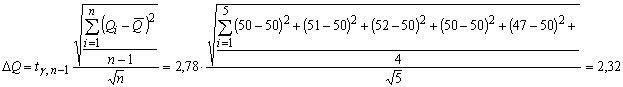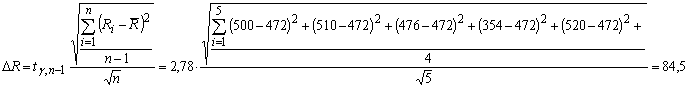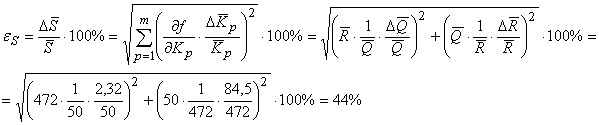|
Версия для печати
1. Введение
Работа химиков, физиков и
представителей других естественно-научных профессий часто связана с
выполнением количественных измерений различных величин. При этом возникает
вопрос анализа достоверности получаемых значений, обработки результатов
непосредственных измерений и оценки погрешностей расчетов, в которых
используются значения непосредственно измеряемых характеристик (последний
процесс также называется обработкой результатов косвенных измерений). По целому ряду объективных причин знания
выпускников химического факультета МГУ о расчете погрешностей не всегда
достаточны для правильной обработки получаемых данных. В качестве одной из
таких причин можно назвать отсутствие в учебном плане факультета курса по
статистической обработке результатов измерений.
К
данному моменту вопрос вычисления погрешностей, безусловно, изучен
исчерпывающе. Существует большое количество методических разработок,
учебников и т.д., в которых можно почерпнуть информацию о расчете
погрешностей. К сожалению, большинство подобных работ перегружено
дополнительной и не всегда нужной информации. В частности, большинство
работ студенческих практикумов не требует таких действий, как сравнение
выборок, оценка сходимости и др. Поэтому кажется целесообразным создание
краткой разработки, в которой изложены алгоритмы наиболее часто
употребляемых вычислений, чему и посвящена данная разработка.
2. Обозначения, принятые в данной работе
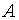 -измеряемая величина, -измеряемая величина, 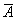 -среднее значение измеряемой величины, -среднее значение измеряемой величины, 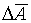 - абсолютная погрешность среднего значения измеряемой
величины, - абсолютная погрешность среднего значения измеряемой
величины, 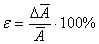 - относительная
погрешность среднего значения измеряемой величины. - относительная
погрешность среднего значения измеряемой величины.
3. Расчет погрешностей непосредственных измерений
Итак, предположим, что были
проведены n измерений
одной и той же величины 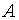 в
одних и тех же условиях. В этом случае можно рассчитать среднее значение
этой величины в проведенных измерениях: в
одних и тех же условиях. В этом случае можно рассчитать среднее значение
этой величины в проведенных измерениях:
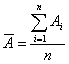 (1) (1)
Как вычислить погрешность 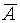 ? По следующей формуле: ? По следующей формуле:
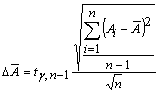 (2) (2)
В этой формуле используется
коэффициент Стьюдента 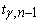 . Его значения при разных доверительных вероятностях и
значениях . Его значения при разных доверительных вероятностях и
значениях 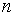 приведены в
таблице. приведены в
таблице.
3.1. Пример расчета погрешностей непосредственных
измерений:
Задача.
Проводили измерения длины 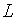 металлического бруска. Было сделано 10
измерений и получены следующие значения: 10 мм, 11 мм, 12 мм, 13 мм, 10 мм,
10 мм, 11 мм, 10 мм, 10 мм, 11 мм. Требуется найти среднее значение металлического бруска. Было сделано 10
измерений и получены следующие значения: 10 мм, 11 мм, 12 мм, 13 мм, 10 мм,
10 мм, 11 мм, 10 мм, 10 мм, 11 мм. Требуется найти среднее значение 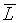 измеряемой величины (длины бруска) и его
погрешность измеряемой величины (длины бруска) и его
погрешность 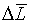 . .
Решение.
С использованием формулы (1)
находим:
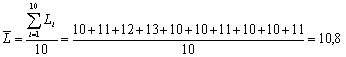 мм мм
Теперь с использованием формулы (2) найдем абсолютную
погрешность 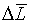 среднего значения среднего значения 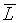 при доверительной вероятности при доверительной вероятности 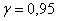 и числе степеней
свободы и числе степеней
свободы 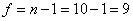 (используем
значение (используем
значение 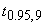 =2,262, взятое из таблицы): =2,262, взятое из таблицы):
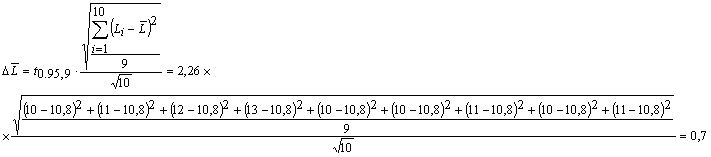
Запишем результат:
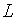 =10,8±0,70.95 мм =10,8±0,70.95 мм
4. Расчет погрешностей косвенных измерений
Предположим, что в ходе эксперимента
измеряются величины 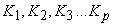 , а затем c использованием полученных значений вычисляется
величина , а затем c использованием полученных значений вычисляется
величина 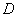 по формуле по формуле 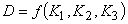 .
При этом погрешности непосредственно измеряемых величин рассчитываются так,
как это было описано в пункте 3. .
При этом погрешности непосредственно измеряемых величин рассчитываются так,
как это было описано в пункте 3.
Расчет среднего значения
величины 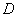 производится по
зависимости производится по
зависимости 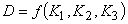 с использованием средних значений
аргументов с использованием средних значений
аргументов 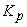 . .
Погрешность величины 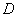 рассчитывается по
следующей формуле: рассчитывается по
следующей формуле:
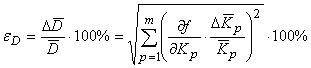 , (3) , (3)
где 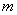 -
количество аргументов -
количество аргументов 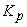 , , 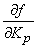 - частные производные функции - частные производные функции 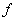 по аргументам по аргументам 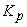 , ,
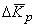 - абсолютная
погрешность среднего значения аргумента - абсолютная
погрешность среднего значения аргумента 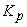 . .
Абсолютная погрешность, как и в
случае с прямыми измерениями, рассчитывается по формуле 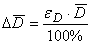 . .
4.1. Пример расчета погрешностей непосредственных
измерений:
Задача.
Было проведено 5 непосредственных измерений величин 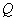 и и 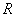 . Для величины . Для величины 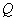 получены значения: 50, 51, 52, 50, 47; для
величины получены значения: 50, 51, 52, 50, 47; для
величины 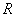 получены значения:
500, 510, 476, 354, 520. Требуется рассчитать значение величины получены значения:
500, 510, 476, 354, 520. Требуется рассчитать значение величины 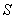 , определяемой по формуле , определяемой по формуле 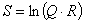 и найти погрешность
полученного значения. и найти погрешность
полученного значения.
Решение.
По формуле (1) найдем средние
значения величин 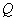 и и 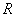 : :
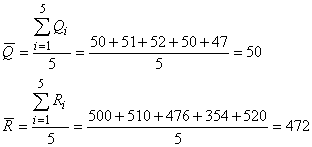
Вычисляем 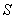 : :
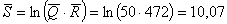
Находим
в таблице при доверительной вероятности 0,95 и числе степеней свободы 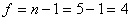 значение значение 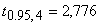 . По формуле (2) рассчитываем погрешности средних
значений величин . По формуле (2) рассчитываем погрешности средних
значений величин 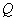 и и 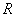 : :
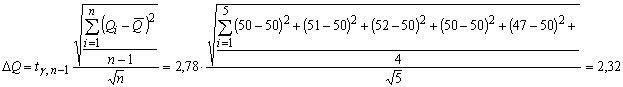 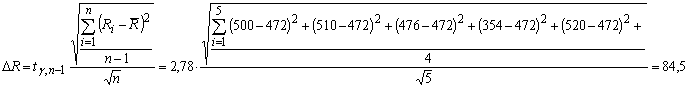
С использованием формулы (3)
находим относительную погрешность среднего значения величины 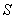 : :
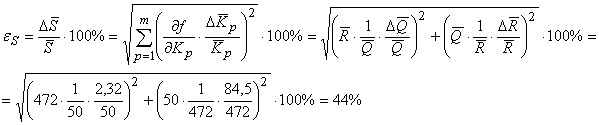
Найдем абсолютную погрешность
среднего значения величины 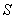 : :
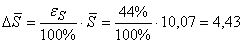
Запишем результат:
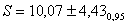
© Баронов С.Б.
Версия для печати
|








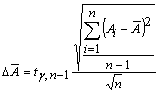
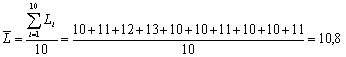 мм
мм