Конспект лекций по математическому анализу. 3 семестр, лектор Ю.Н. Макаров.
Лекции 1,2
Ряды. Дифференциальные уравнения.
Ряды.
Примеры рядов.
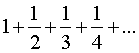 Гармонический
ряд.
Гармонический
ряд.
x(a)= 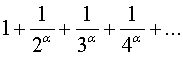 Дзета
функция Риммана.
Дзета
функция Риммана.
А=а1+а2+а3+…= 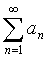
Числовой ряд —бесконечная упорядоченная
сумма чисел.
1-1+1-1+1-1+1-1+…
Аn=а1+а2+а3+…+аn
{An}—последовательность частичных сумм.
Числовой ряд А сходится, если ![]() —сумма сходящегося числового рядя. Если
—сумма сходящегося числового рядя. Если![]() , то ряд А расходится.
, то ряд А расходится.
1+2+3+4+5+… (расходится к бесконечности)
В целом различают несколько основных типов задач:
1) Исследование сходимости ряда.
2) Нахождение суммы.
3) Разложение данной функции в ряд.
Например.
Критерий Коши сходимости ряда.
![]()
" e>0 $ n0 , такое что "n>m³n0: |An-Am|<e.
An=a1+a2+…+an
Am=a1+a2+…+am следовательно An-Am=am+1+…+an
" e>0 $ n0, такое что "n>m³n0 => | am+1+…+an |<e.
Тогда говорят, что последовательность An—фундаментальна.
Пример
![]() Гармонический ряд.
Гармонический ряд.
Зафиксируем e=0.5, m³n0, n=2m
| am+1+…+an |= ![]() =>ряд
расходится.
=>ряд
расходится.
Всего m
слагаемых
|an|<e~ ![]() —необходимый признак сходимости числового ряда.
—необходимый признак сходимости числового ряда.
Д-во: n=m+1 "e>0, $ n0 =>"n³n0:
Следствие 1 А=
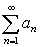 В=
В=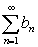
$ n1:" n³n1 => an=bn
Тогда A~B (либо оба сходящиеся либо оба расходящиеся)
n0³n1 | am+1+…+an
|=| bm+1+…+bn |
Следствие 2
A= 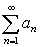 B=
B=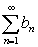 , bn=
, bn=kan
Следствие 3 Если
![]() сходится, то
сходится, то ![]() сходится. При этом говорят, что ряд
сходится. При этом говорят, что ряд ![]() сходится абсолютно.
сходится абсолютно.
| am+1+…+an
|≤|am+1|+|am+2|+…+|an|<e an>0
Достаточные признаки сходимости знакопостоянных рядов.
Признаки сравнения.
а) A= ![]() , B=
, B=![]()
![]()
0<an≤bn
B—сход. =>A—сходится
Для
доказательства применим критерий Коши:
| am+1+…+an |=am+1+am+2+…+an≤bm+1+bm+2+…+bn<e
б) предельный
![]()
Доказательство: из существования предела ![]() следуют
неравенства:
следуют
неравенства:
![]()
![]() тогда по признаку сравнения (а) A~B
тогда по признаку сравнения (а) A~B
Пример. ζ(α)= 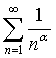 , рассмотрим как ведёт себя этот ряд в зависимости от
α. При α=1 ряд расходится (гармонический).(Было доказано ранее).
, рассмотрим как ведёт себя этот ряд в зависимости от
α. При α=1 ряд расходится (гармонический).(Было доказано ранее).
Для α<1 =>![]() расходится по признаку сравнения
а.
расходится по признаку сравнения
а.
Для α>1
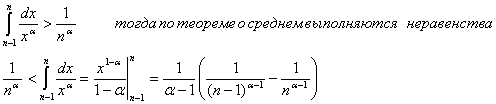
![]()
Пусть![]()
![]()
![]() , т.е. В— сходится, значит по
признаку сравнения ряд ζ(α) при α>1 то же сходится.
, т.е. В— сходится, значит по
признаку сравнения ряд ζ(α) при α>1 то же сходится.
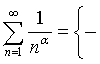 Таким
образом
Таким
образом
α≤1 расходится
ζ(α)=
α>1 сходится
в) признак Деламбера
Пусть ![]() , an>0,
n=1,2,3…, Тогда:
, an>0,
n=1,2,3…, Тогда:
l<1
=>A сходится
l>1
=>A расходится
l=1 =>вопрос
о сходимости остаётся открытым
Д-во
1) l<1, l+e<1, ![]() , n≥n0
, n≥n0
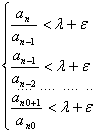
Перемножая все эти неравенства получим: ![]() значит
an<c(l+e)n,n>n0
значит
an<c(l+e)n,n>n0
т.к. l+e<1 то ряд сходится (по ризнаку сравнения а).
2) l>1
=> an+1>an=> an не стремится к нулю => ряд расходится.Т.к не выполняется необходимый
признак сходимости ряда.
Признак Коши (радикальный).
Пусть А= ![]() , an>0
, an>0
и $![]() тогда при l<1 А
сходится, l>1 А
расходится, при l=1 вопрос
о сходимости ряда остаётся открытым.
тогда при l<1 А
сходится, l>1 А
расходится, при l=1 вопрос
о сходимости ряда остаётся открытым.
Д-во
1)l<1
Выберем e : e+l<1
тогда из определения предела:
![]() , значит an<(l+e)n, n³n0 полученна
геомнтрическая прогрессия с q<1 следовательно, ряд сходится (q=λ+ε).
, значит an<(l+e)n, n³n0 полученна
геомнтрическая прогрессия с q<1 следовательно, ряд сходится (q=λ+ε).
2)l>1
![]()
an>1, n ³n0 значит,
![]() , следовательно, не выполнен необходимый признак
сходимости числового ряда.
, следовательно, не выполнен необходимый признак
сходимости числового ряда.
Пример:
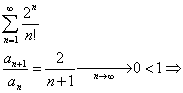 ряд сходится (по
Деламберу)
ряд сходится (по
Деламберу)
Признак сравнения 3.
Пусть А= ![]() , В=
, В=![]() , an>0, bn>0.
, an>0, bn>0.
![]()
тогда A~B
Д-во:
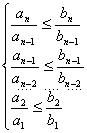
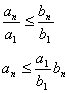 После
почленного перемножения получим:
После
почленного перемножения получим:
так
как a1/b1=const, и B
сходится,
то и А сходится.
Признак Куммера.
![]()
Пусть А=
, an>0 (" n³n0), и {bn} последов-ть чисел, bп>0 такая, что ряд
![]() расходится, и $
расходится, и $ ![]() . Тогда если δ>0 то ряд А сход., если δ<0
то ряд А расходится, если δ=0, то вопрос о сходимости рядя остаётся
открытым.
. Тогда если δ>0 то ряд А сход., если δ<0
то ряд А расходится, если δ=0, то вопрос о сходимости рядя остаётся
открытым.
Д-во.
1)δ>0, выберем e=δ/2 тогда, по определению предела
bn*an/an+1-bn+1>δ-e=δ/2 "n³n0
обозначим cn=anbn-an+1bn+1>δ*an+1/2
и докажем сходимость ряда ![]() , так как cn=anbn-an+1bn+1= δ *an+1/2>0,
то
, так как cn=anbn-an+1bn+1= δ *an+1/2>0,
то
anbn>an+1bn+1![]() , так как {anbn}
монотонно убывающая, ограниченная нулём послед..
, так как {anbn}
монотонно убывающая, ограниченная нулём послед..
Sn=c1+…cn=(a1b1-a2b2)+(a2b2-a3b3)+…+(anbn-an+1bn+1)=a1b1-an+1bn+1![]()
значит ряд cn сходится,
δan+1/2 тоже
сходится (по признаку сравнения) т.к. δ/2=const, то и
исходный ряд сходится => A сходится.
2)δ<0 тогда,
bn*an/an+1-bn+1<0 => ![]() ,
, ![]() "n³n0, значит
"n³n0, значит
по условию ряд 1/bn
—расходится, а значит по признаку сравнения 3 расходится и исследуемый ряд А.
Следствие 1 (признак Деламбера).
Возьмём bn=1, тогда
![]()
![]()
![]()
Если δ>0, то l<1 и ряд А сходится.
δ<0,
то l>1 и
ряд А расходится.
Следствие 2 (признак Раабе)
Пусть bn=n
![]() ,
, ![]() ,
, ![]()
обозначим α=δ+1,
тогда ![]() , значит при α>1 (δ>0) ряд сходится, при
α<0(δ<1)рас.
, значит при α>1 (δ>0) ряд сходится, при
α<0(δ<1)рас.
Следствие 3.
![]() => A-расходится.
=> A-расходится.
Применим к исслед. ряду признак Куммера (bn=n*ln(n) (доказательство
расходимости данного ряда см. ниже). Тогда
bnan/an+1-bn+1=n*ln(n)*(1+1/n+en)-(n+1)ln(n+1)=(n+1)(ln(n)-ln(n+1))+n*ln(n)*en=
=-nln(1+1/n)-ln(1+1/n)+n*ln(n)*en→-1,
т.к. первое из слагаемых стремится (при n стремящемся
к бесконечности) к-1, второе к 0, и 3 к нулю (т.к.lnn/n-> к
0).
Признак Гауса.
Пусть ![]() , важно, что бы остаток был именно в таком виде.
, важно, что бы остаток был именно в таком виде.
Тогда,
1) β<1 A —расх.
2) β>1 A —сход.
3) β=1 α≤1 A — расх.
α>1 A —сход. Доказательство следует из следствий 1-3.
Пример.
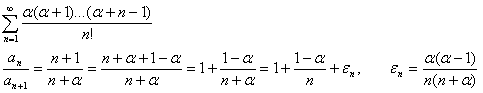
1-α>1
~ α<0, A —сход.
1-α<1 ~
α>0, A —расх.
При α=0 ряд состоит
только из нулевых слагаемых, а следовательно схходится..
Интегральный признак. (Коши-Маклорена)
Пусть ![]() - непрерывная,
неотрицательная, монотонно убывающая функция, определенная при
- непрерывная,
неотрицательная, монотонно убывающая функция, определенная при ![]() (или начиная с
некоторого x>0). Тогда ряд
(или начиная с
некоторого x>0). Тогда ряд ![]() ~
~![]()
Д-во.
Лемма.
Пусть An=a1+…+an — частичная сумма.Тогда ряд сходится тогда, когда An<c c=const. Эта
лемма верна, так как в этом случае последовательность An убывающая
и ограниченная.
Тогда ![]() , или
, или ![]() . Поэтому если
. Поэтому если ![]() сходится, то
сходится, то
![]() . Тогда
. Тогда ![]()
![]() и
и ![]() ,
, ![]() ряд сходится.
ряд сходится.
Пусть теперь наоборот, известно, что ряд сходится. Тогда ![]() . Взяв произвольное
. Взяв произвольное ![]() выберем
выберем ![]() так, чтобы
так, чтобы ![]() . Тогда
. Тогда ![]() . Значит,
. Значит, ![]() сходится.
сходится.
Пример.
![]() ~
~![]() => ряд сходится при
α>1, и расходится при α≤1.
=> ряд сходится при
α>1, и расходится при α≤1.
Расходимость ряда nlnn
![]()
![]() => ряд расходится.
=> ряд расходится.