Лекция №3.

27.09.2002

Знакопеременные ряды

Пусть 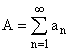и ряд сходится то А также сходится и при этом говорят, что ряд А сходится абсолютно.

Если 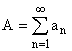сходится, – расходится, то А сходится условно.

ПРИМЕР:

Ряд Лейбница: сходится условно (неабсолютно), так как гармонический ряд расходится.

Признак Лейбница.

Пусть дан знакочередующийся ряд

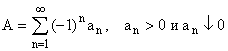(монотонно стремится к 0), тогда А сходится.

Доказательство.

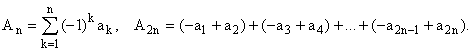
Т.к.

.

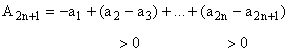, , то есть последовательность частичных сумм убывает, а возрастает.

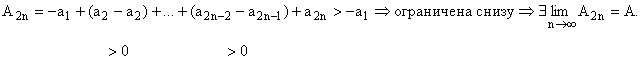Каждая из последовательностей ограничена и .

Следовательно, .

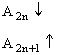
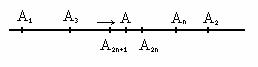
Заметим, что:

.

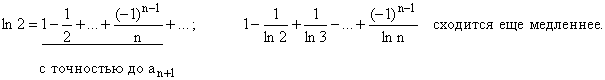
ПРИМЕР (расходящийся знакочередующийся ряд):

не монотонно: 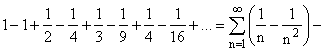расходится.

Вообще, если ряд представим в виде суммы рядов:

1) Если оба ряда сходятся, то их сумма сходится.

2) Если один из рядов сходится, а другой расходится, то их сумма расходится.

3) Если оба ряда расходятся, то ничего определенного о сходимости суммы сказать нельзя.

(Соответствующие примеры рекомендуем придумать свмостоятельно).

Признак Дирихле.

Пусть дан ряд:

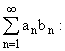
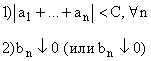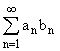тогда сходится.

Доказательство.

По критерию Коши: .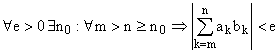

по условию

Используя преобразование Абеля, получим неравенства:

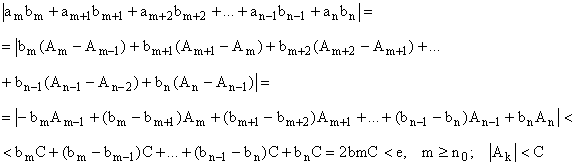
Следовательно, критерий Коши выполнен, поэтому ряд сходится.

Из признака Дирихле следует признак Лейбница:

Если .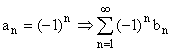

Признак Абеля.

Пусть дан ряд:

:

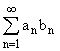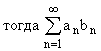
Доказательство.

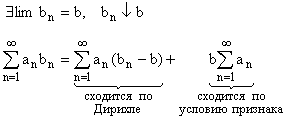Доказано.

ПРИМЕР 1:

:

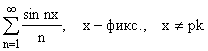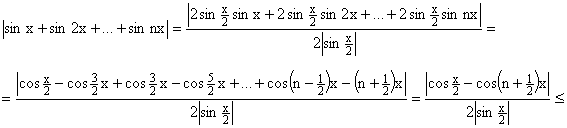
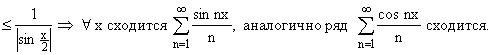
Докажем, что эти ряды сходятся условно:

.

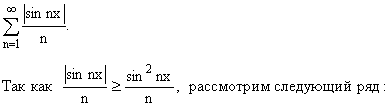
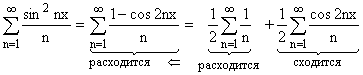Значит, ряд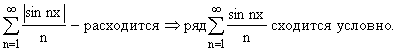

ПРИМЕР 2:

При произвольной перестановке членов условно сходящегося ряда его сумма может измениться:

.

Переставим члены этого ряда следующим образом:

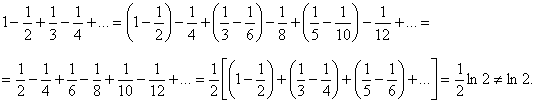
Теорема Римана (без доказательства).

Пусть дан условно сходящийся ряд. Тогда: перестановка слагаемых, такая, что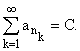

Теорема о перестановке членов абсолютно сходящегося числового ряда.

Пусть ряд сходится абсолютно, 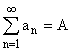. Тогда, для любой перестановки ряда

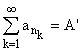новый ряд сходится. При этом, ряд сходится абсолютно и его сумма равна сумме исходного ряда, то есть .

Доказательство.

Рассмотрим два случая:

1)

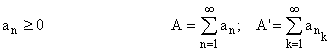
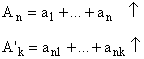
k – фикс., , тогда

.

Аналогично рассматривается ряд А, как полученный перестановкой членов :

. Доказано.

2) Пусть тогда:

;

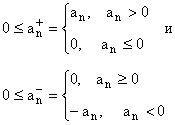
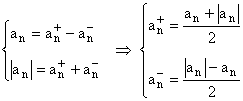– сходится, – сходится, так как ряд А сходится абсолютно .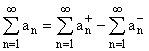

Применяя к и результат из 1), получим полное доказательство.

Доказано.