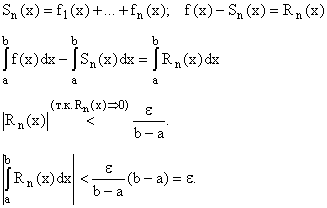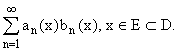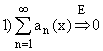Лекция №4.

4.10.2002

Функциональные ряды

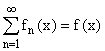– функциональный ряд, функции от , где D – область сходимости ряда.

Примеры функциональных рядов:

1)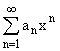– степенной ряд.

2)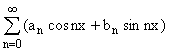 – тригонометрический ряд Фурье

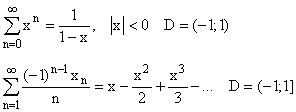
Равномерная сходимость функциональной последовательности и функционального ряда.

Определение равномерной сходимости на множестве функциональной последовательности:

.

Определение.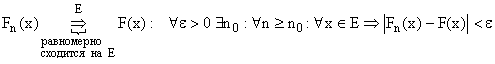

ПРИМЕР:

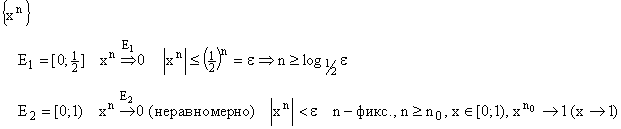
Критерий Коши:

Определение равномерной сходимости функционального ряда на множестве Е:

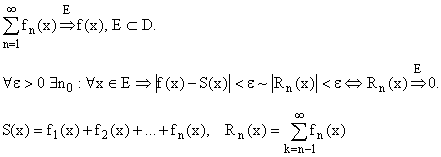
Критерий Коши:.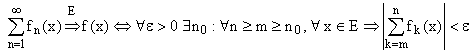

Следствие. Если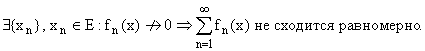

Примеры рядов, не сходящихся равномерно:
1)

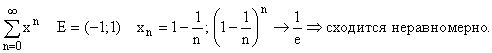
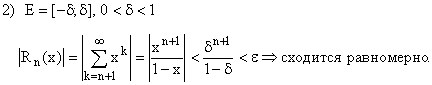
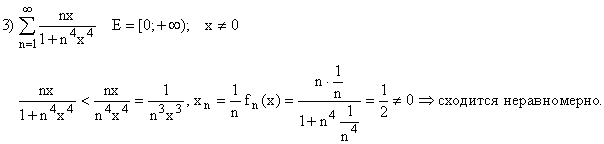
Признак равномерной сходимости.

1) Признак Вейерштрасса (мажорантный признак)

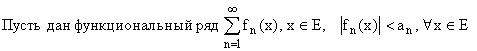
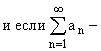сходится, то функциональный ряд 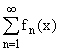сходится равномерно на Е.

Доказательство (по критерию Коши).

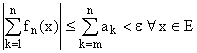
ПРИМЕРЫ:

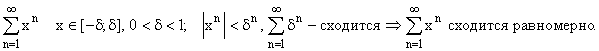
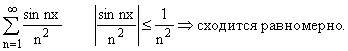
К ряду 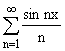признак Вейерштрасса неприменим.

2) Признак Абеля – Дирихле.

Пусть дан функциональный ряд
Абеля Если:	Дирихле Если:
, – монотонная по n последовательность,	по n монотонно, по x равномерно,

То ряд 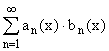сходится равномерно на Е.

ПРИМЕРЫ:

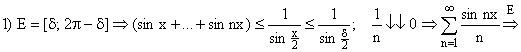
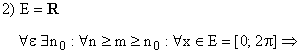
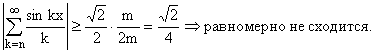
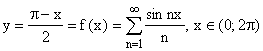(без доказательства).

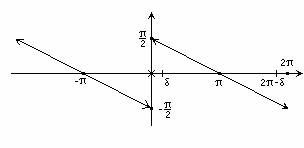
Теорема о непрерывности суммы функционального ряда.

Доказательство.

Докажем, что

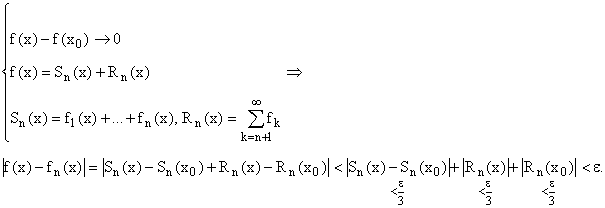
Доказано.

Теорема об интегрировании функционального ряда.

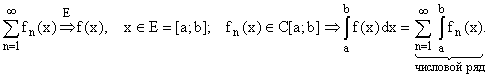
Доказательство.