Лекция 5
Дифференцирование функциональных рядов
Теорема: ![]() fn(x) → f(x), x
fn(x) → f(x), x![]() O(a),
O(a), ![]() fn’(x)
fn’(x) ![]() C(O(a)),
C(O(a)), 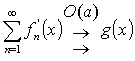
Тогда f(x)![]() D(O(a))
и f’(x)=g(x),
x
D(O(a))
и f’(x)=g(x),
x![]() O(a)
O(a)
Доказательство. (на основании теоремы об интегрировании функционального ряда)
![]() fn’(t)=g(t), t
fn’(t)=g(t), t![]() [a,x]
– непрерывная функция, так как ряд
[a,x]
– непрерывная функция, так как ряд ![]() fn’(t) равномерно сходится на
O(a). На основании теоремы
об интегрировании функционального ряда этот ряд можно проинтегрировать почленно и получить равномерно сходящийся на O(a) ряд.
fn’(t) равномерно сходится на
O(a). На основании теоремы
об интегрировании функционального ряда этот ряд можно проинтегрировать почленно и получить равномерно сходящийся на O(a) ряд.
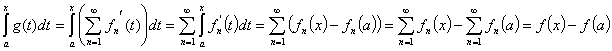
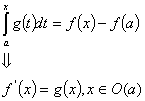
Степенные ряды
Степенными рядами называются ряды вида ![]() , где an,
x0 –постоянные,
x – переменная.
, где an,
x0 –постоянные,
x – переменная.
Мы будем рассматривать ряды с x0=0, т.е. ![]()
1 теорема Абеля. Пусть ![]() сходится при некотором x0. Тогда для
сходится при некотором x0. Тогда для![]() h<
h<![]() ряд
ряд ![]() сходится равномерно на [-h;h]
сходится равномерно на [-h;h]
Доказательство. Так как ![]() сходится, то
сходится, то ![]() , где M>0
– некоторая постоянная.
, где M>0
– некоторая постоянная.
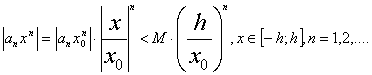
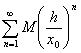 сходится
сходится ![]() по признаку Вейерштрасса
по признаку Вейерштрасса 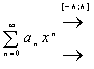
Следствие: 1) ![]()
Область сходимости степенного ряда
D=![]() , где R – радиус сходимости.
, где R – радиус сходимости.
Любой степенной ряд сходится в точке x=0. В остальных случаях ряд
сходится при всех ![]() , если R
– радиус сходимости (точная верхняя грань множества x, для которых ряд сходится)-существует. Если точной верхней грани нет, то полагают
, если R
– радиус сходимости (точная верхняя грань множества x, для которых ряд сходится)-существует. Если точной верхней грани нет, то полагают ![]() - ряд сходится на всей
числовой прямой.
- ряд сходится на всей
числовой прямой.
Приведем примеры:
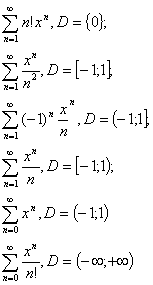
Чтобы найти радиус сходимости, можно воспользоваться признаками сходимости знакопостоянных рядов Даламбера либо Коши.
Признак Даламбера:
![]()
![]()
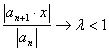
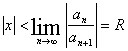
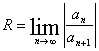
Признак Коши: ![]()
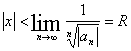
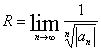
Примечание. Если ни один из
указанных пределов не существует, то нужно положить радиус сходимости равным нижнему
пределу (наименьшему частичному пределу) выражения для R.
Пример. 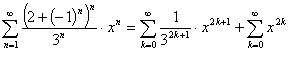
![]()
![]() R=1
R=1
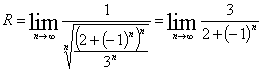 не существует.
не существует.
2 теорема Абеля.
Ряд ![]() сходится в точке x=x0 . Тогда ряд
сходится в точке x=x0 . Тогда ряд ![]() сходится равномерно на отрезке [0;x0] (или [x0;0] если x0<0).
сходится равномерно на отрезке [0;x0] (или [x0;0] если x0<0). 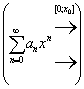
Доказательство. 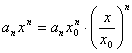
1) ![]() по условию
по условию
2) ![]()
![]()
![]() - невозрастающая по n функция.
- невозрастающая по n функция.
Следствия:
1) ![]() , D –
область сходимости
, D –
область сходимости
![]()
![]()
![]()
2)![]() , D –
область сходимости
, D –
область сходимости
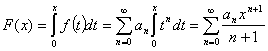
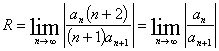
![]()
![]()
3)![]()
![]()
Ряды Тейлора
Применяя последовательно теорему о почленном дифференцировании степенного ряда, получим соотношение для n-го коэффициента ряда.
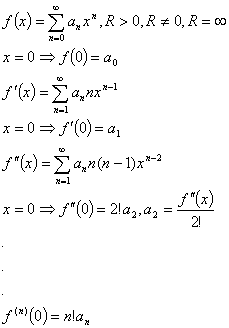
![]()
![]() -
коэффициенты степенного ряда Тейлора
-
коэффициенты степенного ряда Тейлора
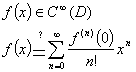 - в общем случае неверно, т.е. ряд Тейлора для функции f(x) не всегда совпадает с самой
функцией.
- в общем случае неверно, т.е. ряд Тейлора для функции f(x) не всегда совпадает с самой
функцией.
Пример.
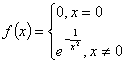
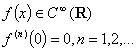
Пусть ![]()
и ![]() ; тогда
; тогда ![]()
Доказательство. По формуле Тейлора с остатком в форме Лагранжа получим:
![]()
![]()
![]()
![]()
![]()