Лекция 8
1) 
Разложим на множители:
при x =a 1 =A( b-a )
A=–1/(a–b)
при x = b 1= B(a–b) B=1/(a–b)
В точке (0,0) частное
решение исходного уравнения: 
2)Найдем закон Т(t) остывания кипящей воды до комнатной температуры (tкомн=200) и время достижения 400, если до 600 вода остывает за 20 мин. Известно, что мгновенная скорость остывания линейно зависит от разницы Т и tкомн.
Составим дифференциальное
уравнение: 
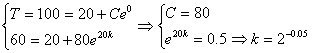
1) Найти количество соли в растворе через время t, если известно, что изначально было 10 кг соли в 100 л воды, но каждую минуту в резервуар поступает 20 л воды, а выливается 20 л раствора.
Vр-ра(t) = 100 + 30t –20t = 100 + 10t x(0)=0, x(t)– количество соли
; 
; 
; при t
= 0 x(t )=10C =
1000
4)Найти точный закон радиоактивного распада, если t0–период полураспада., а x0– начальное количество. Причем известно, что мгновенная скорость распада линейно зависит от мгновенного количества вещества.
Задано, что х (0)=х0; x(t0)= х0/2
; 
Таким образом закон распада: 
Линейное
дифференциальное уравнение 1-го порядка.
такие уравнения в общем виде могут ыть представлены как: 
Пусть y = UV, где U, V– некоторые функции от х, тогда подставляя получаем
Выберем V(x) так, чтобы она
удовлетворяла условию: 
Берем любую функцию,
удовлетворяющую этому уравнению, например, V = V(x) и подставляем в исходное
уравнение 
Пример
Замена: y = UV 
Так как ищем одно любое решение, то при интегрировании не
надо добавлять константу: 
Подставим в исходное уравнение: 
Следовательно, 
Этот метод применим и для нелинейного уравнения: 
, где к– константа
Пусть y = UV, где U, V– некоторые функции от х, тогда подставляя получаем
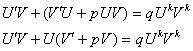
Выберем V(x) так, чтобы она
удовлетворяла условию:
Берем любую функцию,
удовлетворяющую этому уравнению, например, V = V(x) и подставляем в исходное
уравнение 
из последнего уравнения интегрированием находим U, а затем уже зная V(x) находим у.
Пример
Решим дифференциальное уравнение, описывающее прохождение по цепи переменного тока, чтобы найти зависимость мгновенной силы тока от времени.
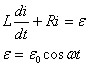
Сделаем замену переменных: 
и подставим
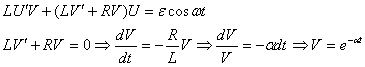
Где примем замену: α=
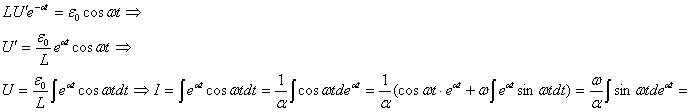
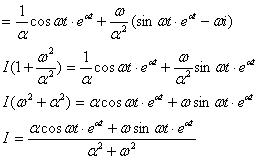
Всегда
можно ввести ω0 (собственная
частота): 
При больших t стремится к нулю 
Уравнение Лагранжа имеет вид 
, где 
-
дифференцируемая функция. Решение
находится в параметрическом виде
Уравнение Клеро – это частный случай уравнения Лагранжа: 
. Вводя параметр 
, получаем 
(т.е. 
, как раз оставшийся случай), 
или 
. Тогда, если 
, то 
и 
- это общее решение
уравнения Клеро (прямые линии). Если же 
, то 
. Тогда 
.
Пример
Общее решение
уравнения будет: 
; особое решение : 0=x + 2C
Проверим, что
последняя функция действительно является решением исходного уравнения: 
Дифференциальное уравнение n-ного порядка
Общее решение в неявном виде (должно содержать n произвольных независимых
постоянных): 
Либо общее решение может быть найдено в явном виде: 
Пример
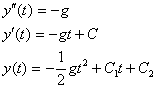Если задать начальные условия: y (0) = y0 , V(0)=V0 , то V0=С1 y0=С2
Чтобы решить задачу Коши для
дифференциального уравнения 1-го порядка: 
, т.е. найти функцию-решение (интегральную кривую),
проходящую через данную точку, достаточно задать 1 условие: y(х0)= y0.
Но в случае дифференциального уравнения n-го порядка задать надо n условий. В этом состоит задача Коши.
Теорема.
Пусть функция 
определена и
непрерывна в области 
. Пусть 
непрерывны в 
. Тогда задача Коши,
состоящая в нахождении решения уравнения 
с начальными условиями
(где точки 
принадлежат области ) имеет, притом единственное решение, в окрестности x=x0. Теорема сформулирована без доказательства.