Лекция 9

 

Дифференциальное уравнение n-ного порядка.

Дифференциальным уравнением n-ного порядка называется уравнение вида:  для нахождения единственного решения неоюходимо знать начальные условия

Уравнения допускающие понижение порядка.

Можно отыскать решение этого уравнения, если уравнение имеет один из нижеследующих  видов:

1) , решается двойным интегрированием.

2) ,  делаем замену y’=p=p(x), y’’=p’

3) , тогда

Пример 1:

y’’y=(y’)2

обозначим , тогда pp’y=p2

рассмотрим несколько случев

1)      p=0 => y=c

2)      p¹0 => p¢y=p или p¢/p=1/y => dp/p=dy/y

lnp=lny+c, p=cy, y¢=cy, dy/y=cdx =>

Линейные дифференциальные уравнения

Линейным дифференциальным уравнением называется уравнение вида:

 (1)

При q=0, уравнение называется однородным, q¹0 неоднородным.

y¢+py=q –дифференциальное уравнение первого порядка.

y¢¢+p1y¢+p2y=0. если p1 и p2 непрерывны в рассматриваемой области, то $ ! 1-ая диф. кривая => единственное решение дифференциального уравнения.

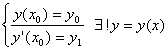
Обозначим левую часть  уравнения (1) при q(x)=0 L(y)=>L(y)=0.

Отметим два свойства L(y).

1)      L(y1+y2)=L(y1)+L(y2)

2)      L(Cy)=CL(y)

Линейная зависимость функций

Функции y1,…,yn называются линейно зависимыми, если $ λ1,…,λn (|λ1|+…+|λn|¹0) такие что  соответственно функции называются линейно независимыми если не удовлетворяют уравнению (1).

Определитель Вронского.

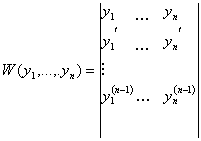
Теорема 1.

Если функции y1(x),…,yn(x)(все функции и их производные непрерывны и существуют до n-1 го порядка) линейно зависимы, то  =0.

Д-во.

Так как функции линейно зависимы, то после дифференциирования получим:

                                                                                                                                            ,                                                                                                                           Эта система имеет ненулевое решение ó когда определитель этой системы равен 0. А этот определитель и есть определитель Вронского.

Если W¹0  хотя бы в одной точке то функции линейно независимы.

Пример 1

             Покажем, что если определитель равен нулю, то функции необязательно линейно зависимы.   ,     

 

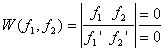
Рассмотрим произвольную точку x0>0.

Утв. Если функции линейно независимы, то W=0

        Если W=0, то неизвестно зависимы функции или нет.

         Если W¹0 в какой-либо точке, то функции линейно независимы.

Теорема 2 Пусть решения уравнения  и  тогда

Следствие: если хотя бы в одной точке (a,b) тогда " x '(a,b) W(x)¹0.

Д-во

Так как W=0 в x0, то 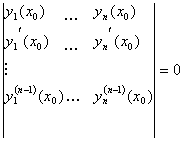 так как определитель =0 то его строки и столбцы и строки линейно зависимы (их линейная комбинация равна 0). Значит

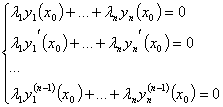
Рассмотрим функцию y= L(y)=0, т.е. y- решение дифференциального уравнения. Следовательно,  (*)  (первая строка в системе). Решение  удовлетворяет (1) но начальным условиям удовлетворяет только одно решение (по теореме о существовании единственного решения). Получаем, что W=0 " x э (a,b).

Пример 1

y(n)=0 Решения:y1=1, y2=x, y3=x2,…,yn=xn-1

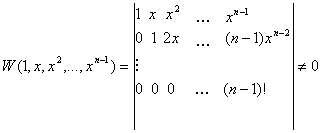 этот определитель равен произведению чисел на главной диагонали (а все эти числа отличны от нуля), следовательно определитель отличен от нуля, следовательно функции линейно независимы.

Пример 2.

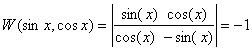 Значит функции линейно независимы.

Пример 3

 

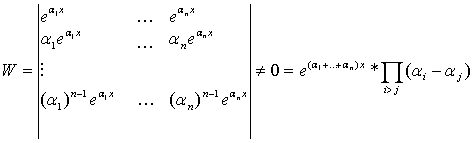
Фундаментальная система решений есть полная система решений дифференциального уравнения.