Лекция №10.

4.10.2002

Фундаментальная система решений линейного

однородного уравнения

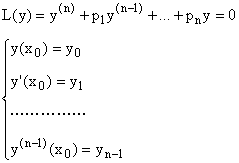Начальные условия:

Определение: Любые n линейно независимых решений линейного однородного дифференциального уравнения n-ного порядка называется фундаментальной системой решений этого уравнения.

Теорема: Решения уравнения образуют фундаментальную систему решений этого уравнения тогда и только тогда, когда их определитель Вронского отличен от 0 хотя бы в одной точке .

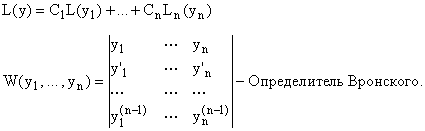
Теорема: Для любого линейного однородного дифференциального уравнения существует фундаментальная система его решений.

Доказательство: Пусть

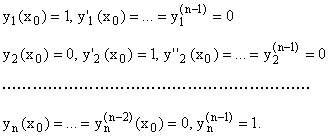
Тогда определитель Вронского запишется так:

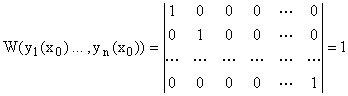
Систем линейно независима, поэтому она образует фундаментальную систему решений:

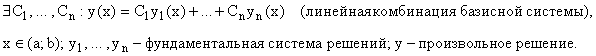
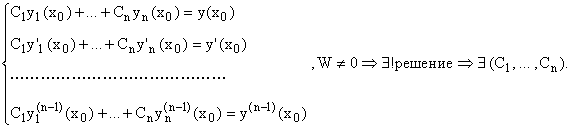
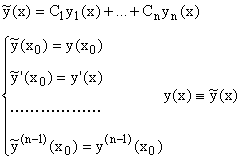
Линейное однородное дифференциальное уравнение с постоянными коэффициентами:

Частные случаи:

n = 2:

:

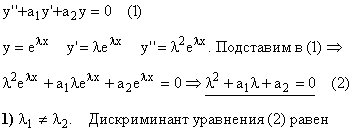
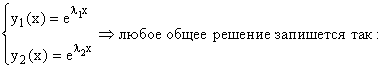
ПРИМЕР:

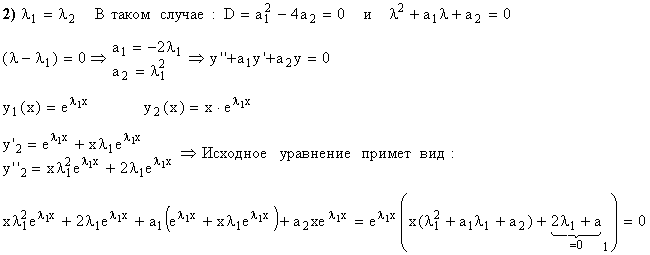
Поэтому определитель Вронского запишется так:

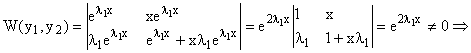
Общее решение:

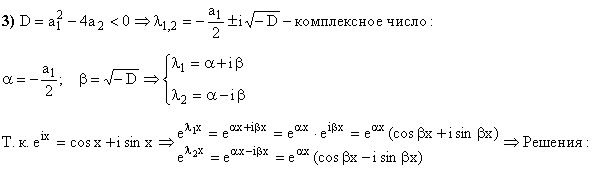
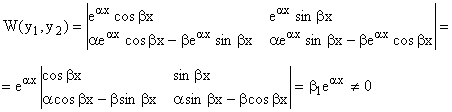
Общее решение:

В общем виде:

Решение надо искать в виде

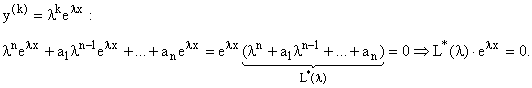
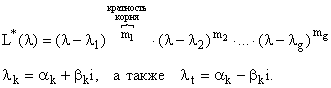
Утверждение: Если следующие m функций (решения уравнения L(x))

– линейно независимы

;

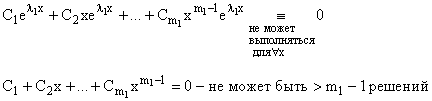
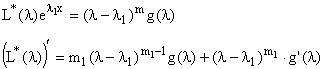
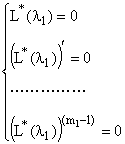(по формуле Лейбница).

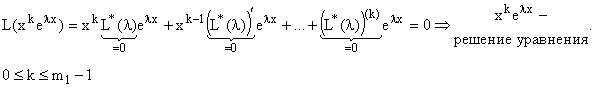
Общее решение – многочлен k-й степени от аргумента в зависимости от вида частного решения:

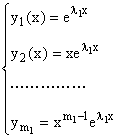
Аналогично находятся фундаментальные решения для остальных корней