Лекция 11
Замечательное свойство определителя Вронского для
определителя 2-го порядка
![]() Пусть у1, у2 –
фундаментальная система решений, тогда:
Пусть у1, у2 –
фундаментальная система решений, тогда:
W(y1, y2) = 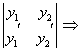
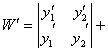
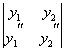 =
= =
=
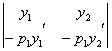 = –p1
= –p1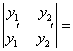 –p1
W(y1, y2)
–p1
W(y1, y2)
Таким образом определитель Вронского функций y1, y2 , удовлетворяющих дифференциальному уравнению второго порядка , удовлетворяет дифференциальному уравнению первого порядка.
![]()
Фундаментальных систем решений может быть много. Выбор фундаментальной системы решений зависит от начальных условий, так как при задании разных начальных условий получаются разные функции, описывающие фундаментальные решения, и соответственно разные значения определителей Вронского, отличающиеся на константу.
Аналогично для ![]()
![]()
Пример
![]() Угадываем корень у1=х
Угадываем корень у1=х
![]()
![]()
![]()
![]() W(y1, y2) =
W(y1, y2) = 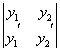
Найдем второе решение у2: W(х, y2) = 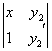 =
=![]()
![]()
Замена: y2
= UV ![]() Одним из решений последнего уравнения будет функция
V = x, подставим ее в исходное:
Одним из решений последнего уравнения будет функция
V = x, подставим ее в исходное: ![]()
![]()
![]()
![]()
![]() общее решение. При С1
≠0 у1 и у2 будут образовывать фундаментальную систему
решений исходного уравнения.
общее решение. При С1
≠0 у1 и у2 будут образовывать фундаментальную систему
решений исходного уравнения.
Решение неоднородного
линейного дифференциального уравнения n-го порядка
L(y)=![]() (1)
(1)
Предположим, что найдена ф.с.р. соответствующего однородного
уравнения (L(y)=q(x)=0): ![]()
Пространство решений неоднородного уравнения уже не является линейным пространством.
Теорема * Пусть
![]() - решение уравнения
- решение уравнения ![]() (1). Тогда любое
другое решение этого уравнения
(1). Тогда любое
другое решение этого уравнения ![]() имеет вид
имеет вид ![]() , где
, где ![]() - решение уравнения
- решение уравнения ![]() , т.е. однородного.
, т.е. однородного.
![]() Вычтем уравнения одно из другого и, вычитая
производные:
Вычтем уравнения одно из другого и, вычитая
производные:
![]()
![]()
Любое решение Y однородного уравнения представляется в виде линейной комбинации ф.р.
Y=y–y0 =![]() , т.е. y
= y0 +
, т.е. y
= y0 +![]() (общее решение неоднородного ).
(общее решение неоднородного ).
Нахождение частного решения неоднородного уравнения.
Оно почти всегда находится, если известна ф.с.р. соответствующего однородного уравнения.
Метод вариации постоянных
Этот метод уже был нами применен для неоднородного уравнения первого порядка.
Вернемся к неоднородному
уравнению ![]() (1). Предположим, что
мы можем найти фундаментальную систему решений
(1). Предположим, что
мы можем найти фундаментальную систему решений ![]() соответствующего
однородного уравнения
соответствующего
однородного уравнения ![]() (2). Тогда, любое решение
(2). Тогда, любое решение ![]() этого уравнения имеет
вид:
этого уравнения имеет
вид: ![]() . Предположим также,
что нам удалось найти некоторое решение
. Предположим также,
что нам удалось найти некоторое решение ![]() уравнения (1). По
теореме * , любое решение
уравнения (1). По
теореме * , любое решение ![]() этого уравнения имеет
вид:
этого уравнения имеет
вид: ![]() (3). Итак, для
нахождения всех решений уравнения (1) требуется найти какое-то одно его решение
(3). Итак, для
нахождения всех решений уравнения (1) требуется найти какое-то одно его решение
![]() . Для этого можно использовать метод вариации постоянных, который состоит в том, что решение
уравнения (1) ищется в виде
. Для этого можно использовать метод вариации постоянных, который состоит в том, что решение
уравнения (1) ищется в виде ![]() (4), где
(4), где ![]() - фундаментальная
система решений уравнения (2). Отметим, что (4) напоминает (3), но имеет
существенное отличие от этого равенства состоящее в том, что в (3) все
- фундаментальная
система решений уравнения (2). Отметим, что (4) напоминает (3), но имеет
существенное отличие от этого равенства состоящее в том, что в (3) все ![]() - постоянные, а в (4)
это – неизвестные функции от
- постоянные, а в (4)
это – неизвестные функции от ![]() . Потребуем, чтобы кроме равенства (4) выполнялись такие
равенства:
. Потребуем, чтобы кроме равенства (4) выполнялись такие
равенства:
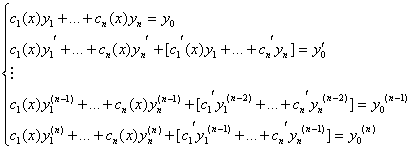
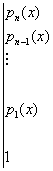 (*) (домножаем и складываем
ур.)
(*) (домножаем и складываем
ур.)
Пусть выражения в квадратных скобках равны нулю, кроме последней скобки, равной q. Тогда при сложении в первом столбце( и в последующих) получится ноль, но в последнем будет q(x).
![]()
![]() Но это равенство
выполняется только в случае выполнения принятой нами системы условий, т.е. если найдены функции Сk (x), удовлетворяющие этой
системе условий(*), то функция y0
есть частное решение неоднородного уравнения.
Но это равенство
выполняется только в случае выполнения принятой нами системы условий, т.е. если найдены функции Сk (x), удовлетворяющие этой
системе условий(*), то функция y0
есть частное решение неоднородного уравнения.
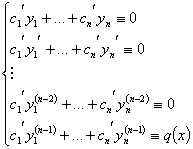
Получили таким
образом обычную систему (*) линейных уравнений, которая имеет единственное
решение, если не равен нулю определитель
системы, т.е. определитель Вронского. Для того, чтобы отыскать ![]() следует
воспользоваться системой (*), рассматривая ее как систему линейных уравнений
относительно неизвестных
следует
воспользоваться системой (*), рассматривая ее как систему линейных уравнений
относительно неизвестных ![]() с определителем
с определителем ![]() .
.
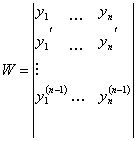 ≠0 Решения
системы (*) можно найти по формулам Крамера.
≠0 Решения
системы (*) можно найти по формулам Крамера.
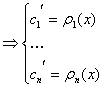 интегрируем и находим
искомые C1,…,Cn.
интегрируем и находим
искомые C1,…,Cn.
Пример
![]()
![]()
![]()
![]()
![]()
![]()
![]() Вычтем одно
уравнение из другого:
Вычтем одно
уравнение из другого: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() –частное решение
неоднородного уравнения
–частное решение
неоднородного уравнения
![]() –общее решение
неоднородного уравнения.
–общее решение
неоднородного уравнения.