Лекция 3
Интеграл Пуассона (интеграл вероятности)
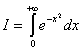
Вычислим с помощью двойного интеграла.
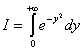 =
=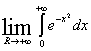 (по определению)
(по определению)
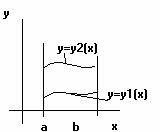
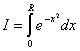 ,
, ![]() ,
, ![]()
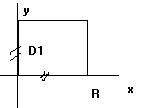
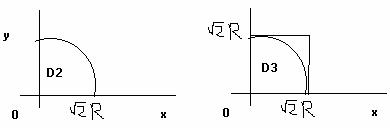
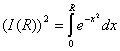
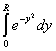 =
=![]() , где D1–квадрат, D1
, где D1–квадрат, D1![]() D2
D2
![]()
![]()
![]()
![]() =В(R)
=В(R)
D1![]() D2
D2![]() D3
D3
C(R)= ![]()
A(R)<B(R)<C(R)
B(R)= 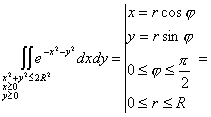
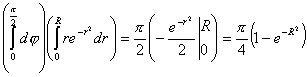
A(R) ![]()
A(R) и C(R) имеют один предел при R![]() , т.к.
, т.к. ![]() . Следовательно,
. Следовательно,
![]()
![]()
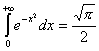
Тройные интегралы
Интегрирование на компакте К
![]()
Определение объема компакта:
Разобьем многогранник Pn , содержащий К, на пирамиды. Суммируя объемы пирамид, найдем объем этого многогранника. Тогда объем заключенного компакта
![]() V(K)
V(K)![]()
свойство: если V(K1![]() K2)=0, тогда V(K1
K2)=0, тогда V(K1![]() K2)=
K2)=![]()
Следовательно, возможно только такое разбиение компакта, при котором объем границ нулевой (по аналогии с двойным интегралом). В этом случае разбиение трехмерного компакта осуществляется поверхностями с нулевым объемом (например, плоскостями):
Т– разбиение компакта: ![]() для
для ![]() .
.
dT–диаметр разбиения: (![]() )
)
S(T)=![]()
![]() =
=![]()
Все свойства для двойных интегралов справедливы для тройных интегралов (доказательства аналогичные). Физический смысл тройного интеграла заключается в том, что если плотность вещества задана функцией f, то масса вещества в определенном объеме– это тройной интеграл функции f по этому объему.
Вычисление тройных
интегралов
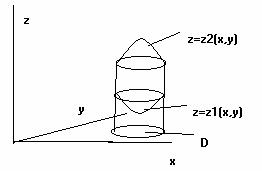
К– компакт-цилиндроид
![]() =
=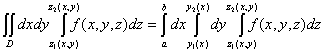
Если область интегрирования К– прямоугольный параллелепипед, а функция представима в виде произведения: f(x,y,z)=f1(x)f2(y)f3(z), тогда
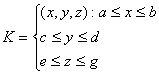
![]() =
=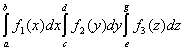
Замена переменных
Аналогично двукратному интегралу, отображение должно быть взаимооднозначным и, следовательно, якобиан
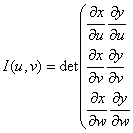
![]()
![]()
![]()
![]() =
=![]()
Пример 1: (цилиндрические координаты)
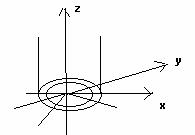
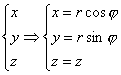
![]()
I(r,![]() ,z)=r
,z)=r
Пример 2: (сферические координаты)
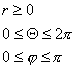 Формулы связи:
Формулы связи: 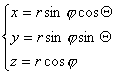 I=
I=![]() (якобиан замены)
(якобиан замены)
Vшара= ![]() =
=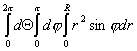 =
=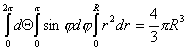
Пример 3:
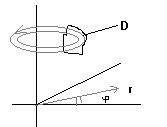
Плоская область D![]() XOZ, вращаем ее вокруг оси Oz в цилиндрических координатах.
XOZ, вращаем ее вокруг оси Oz в цилиндрических координатах.
Объем тела вращения:
V=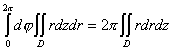
Mz=![]() (статический момент инерции области В относительно
оси Oz)
(статический момент инерции области В относительно
оси Oz)
Mz=S(D)rc, где rc – расстояние от центра тяжести D (плотность области D равна 1).
V=![]()
Таким образом, объем тела вращения области D вокруг неподвижной оси z равен произведению S(D) на длину окружности, описанной центром тяжести области D.
Пример 4: (тор)
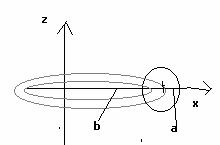
b>a Vтора=![]() , где rc=b.
, где rc=b.