Лекция 4
Криволинейные интегралы.
Выделяют два типа интегралов: первого и второго рода.
Рассмотрим криволинейный интеграл первого рода.
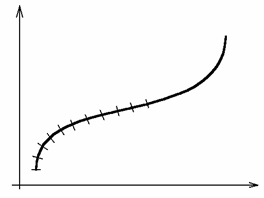
Пусть требуется найти длину кривой на плоскости,
определенной уравнением y=y(x).
Как было доказано во
втором семестре:
 y
y
|L|=∫dl
так как y = y(x), то
L 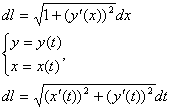
x
Кривая y=y(x) имеет конечную длину, если ![]()
Пример непрерывной кривой, не имеющей конечной длины:
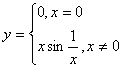 ,где
,где ![]()
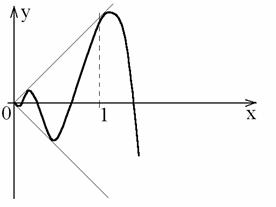
Кривая является синусоидой, заключенной между двумя прямыми ![]() и
и ![]() .
.
Для функции ![]() условие непрерывности
условие непрерывности ![]() в точке х=0
в точке х=0
нарушается. Кривая, заданная уравнением:![]() не имеет конечной длины (доказать самостоятельно)
не имеет конечной длины (доказать самостоятельно)
Опр. По определению, криволинейным интегралом первого (I-го) рода на плоскости называется:
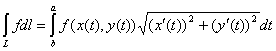 ,где L – кривая, заданная
уравнениями
,где L – кривая, заданная
уравнениями ![]() . Докажем корректность определения:
. Докажем корректность определения:
Сделаем замену: ![]() ,где
,где ![]() и
и ![]()
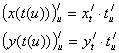 ,где
,где ![]() и
и ![]() ,
,
тогда ![]() ,аналогично и
,аналогично и ![]()
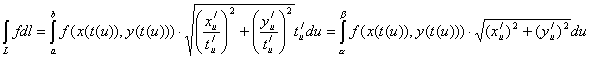 ,
,
Как видно из полученного выражения, определение не зависит от выбора параметра.
 Опр. Кривая
Опр. Кривая ![]() , заданная параметрическими уравнениями
, заданная параметрическими уравнениями ![]() и
и ![]() называется гладкой, если функции
называется гладкой, если функции ![]() и
и ![]() имеют непрерывные
производные, не обращающиеся одновременно в нуль.
имеют непрерывные
производные, не обращающиеся одновременно в нуль.
Опр. Кусочнонепрерывной (кусочногладкой)
кривой называется кривая, которая является непрерывной и состоит из нескольких
гладких кривых.
Свойства кусочнонепрерывной кривой (без доказательства):
![]()
![]() (свойство
аддитивности)
(свойство
аддитивности)
Аналогично кривая ![]() задается системой:
задается системой:

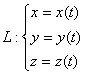 это уравнение
кусочнонеперывной кривой
это уравнение
кусочнонеперывной кривой
Кривую L будем называть кривой по пути АВ,
т.е. начало
L кривой в точке А и конец в точке В.
А В
Заметим, что криволинейный интеграл первого рода не завистит
от того, в каком направлении мы интегрируем по прямой от![]() ,или от
,или от ![]() .
.
Опр. Интеграл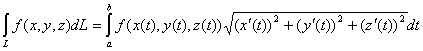 называется криволинейным интегралом первого рода по кривой в
пространстве
называется криволинейным интегралом первого рода по кривой в
пространстве ![]() .
.
Криволинейные интегралы второго типа.
Для начала, как и в случае криволинейных интегралов первого
рода, интеграл второго рода будем рассматривать на плоскости (в![]() ).
).
Криволинейным интегралом второго рода называется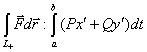 ,
,
где ![]() и
и ![]() ,
, ![]() .
.
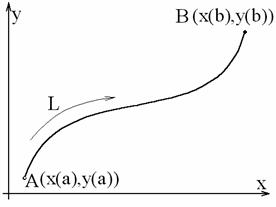 Точки
А и В имеют координаты
Точки
А и В имеют координаты
А(x(a),y(a)) и B(x(b),y(b))
соответственно.
L+ означает, что выбрано
положительное
направление движения по кривой, т.е. то направление, при котором интеграл от А до В имеет положительное значение.
Обозначим ![]() - радиус вектор и
- радиус вектор и
![]()
Работа по перемещению тела из точки А в точку В
в поле ![]() выражается интегралом:
выражается интегралом:
![]()
в этом и есть физический смысл интеграла.
Докажем корректность определения:
Делаем замену t=t(u) и ![]() ,
,
![]() и P зависит
от x,y, которые, соответственно, зависят
от u, а значит интеграл можно представить в виде:
и P зависит
от x,y, которые, соответственно, зависят
от u, а значит интеграл можно представить в виде:
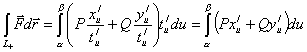
т.е. интеграл не зависит от выбора параметризации.
Свойства:
 10
Является линейным по функции и аддитивным по множеству, т.е.
10
Является линейным по функции и аддитивным по множеству, т.е. ![]() и
и ![]()
А
20 ![]() L+ L- L+=AB
L+ L- L+=AB
L-=BA
В
Физический смысл
этого свойства заключается в следующем утверждении: работа сил в поле в одном направлении, равна работе сил со знаком
минус
в другом направлении
Связь между криволинейными
интегралами 1 и 2 рода.
 В
В
Зададим касательный вектор движения по прямой
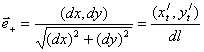
![]()
![]()
![]() ,
, ![]()
![]() А
А
![]() ,а этот интеграл является
интегралом первого типа.
,а этот интеграл является
интегралом первого типа.
Аналогично определим криволинейный интеграл второго рода в ![]() .
.
Рассмотрим векторное поле
![]() , для которого
, для которого ![]() является радиус вектором, тогда
является радиус вектором, тогда
![]() , и
, и
![]()
Кривая L задается системой 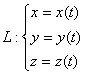 .
.
По определению:
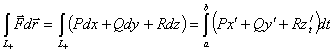 ,
,
а это криволинейный интеграл второго рода в пространстве. Независимость
от выбора параметра доказывается также, как и в ![]() .
.
Пример
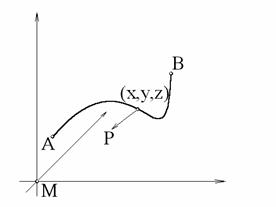 Рассмотрим
пример, в котором точка с массой М находится в начале координат и неподвижна, а
точка m, с массой m, движется по АВ.
Рассмотрим
пример, в котором точка с массой М находится в начале координат и неподвижна, а
точка m, с массой m, движется по АВ.
Вычислить работу по перемещению точки m, приняв гравитационную постоянную
равной ![]() .
.
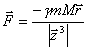 , т.е.
, т.е.
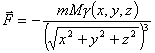
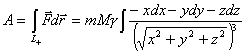
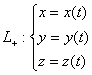 ,а
,а
точки А и В имеют координаты ![]() и
и ![]() соответственно.
соответственно.
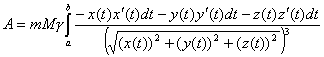
рассмотрим ![]() , тогда
, тогда ![]() , как производная сложной функции от нескольких переменных,
будет равна
, как производная сложной функции от нескольких переменных,
будет равна
![]() ,для вычисления
,для вычисления ![]() , представим
, представим ![]() и
и![]() в виде
в виде
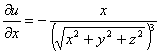 ,
, 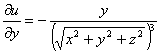 и
и 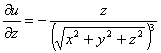 ,соответственно,
,соответственно,
тогда подставив эти выражения в уравнение для ![]() , получаем:
, получаем: 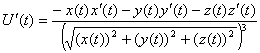 , а так как работа
выражается через определенный интеграл, то подставив это выражение, получаем
, а так как работа
выражается через определенный интеграл, то подставив это выражение, получаем
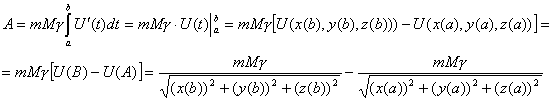
Заметим, что работа в гравитационном поле не зависит от выбора пути, а зависит только от начальной А и конечной В точек этого пути.