Лекция 5

Формула Грина.

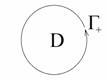В настоящем разделе рассмотрим формулу, связывающую двойной и криволинейный интегралы.

, интеграл называется интегралом по замкнутому контуру.

Условимся называть положительным направлением обхода простого замкнутого контура то, при котором ближайшая к наблюдателю часть области, ограниченной контуром, оказывается лежащей слева от наблюдателя.

Пусть и , т.е.непрерывны на (D) и Г- замкнутый кусочногладкий контур, тогда имеет место формула:

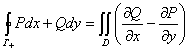,которая называется формулой Грина.

Для вывода формулы будем сводить вычисление интеграла по замкнутой кривой к интегралу от области, заключенной внутри этой кривой.

Разобьем вывод на несколько пунктов:

1) Область D есть криволинейная трапеция:

Докажем равенство

Мы знаем, что

и

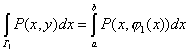, где ,

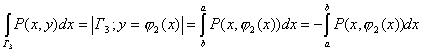
, x = a, dx = 0

Запишем теперь интеграл по контуру в виде 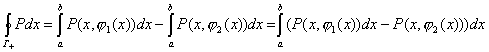, а двойной интеграл будет выглядеть соответственно: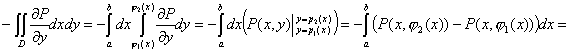

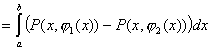, следовательно,

- первая часть равенства доказана.

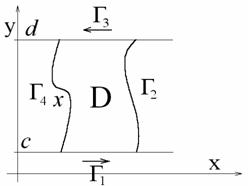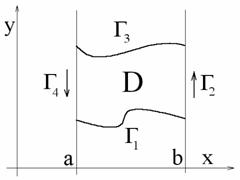
2) Докажем теперь и вторую часть равенства. Пусть D – криволинейная трапеция, изображенная на рисунке:

Запишем теперь интегралы от отдельных участков кривой, причем интегралы от Г₂ и Г₄ будут равны нулю:

,.

Интегралы от Г₁ и Г₃ будут равны соответственно:

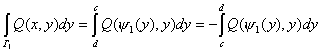
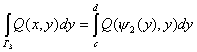, тогда

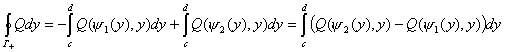Запишем двойной интеграл в виде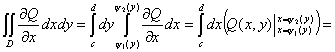

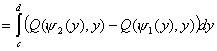, следовательно, мы доказали, что , но ранее мы также доказали, что , следовательно, можно представить как .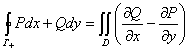

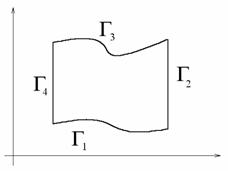
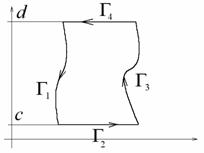
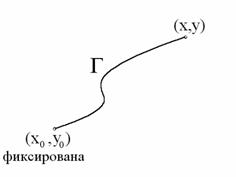
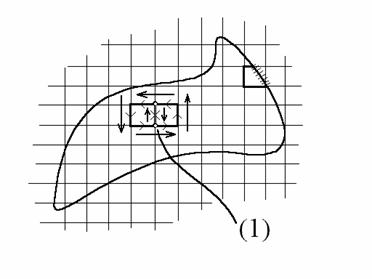Пусть D – произвольная область, ограниченная кусочногладкой кривой. Разобьем D на несколько областей прямыми, как показано на рисунке.

Интеграл по границе двух элементов (1) равен нулю, так как он вычисляется дважды в противоположных направлениях, следовательно, сумма всех криволинейных интегралов будет равна интегралу по границе D.

Рассмотрим теперь некоторые следствия из формулы Грина.

Следствия:

1) Пусть ,

тогда и

2) Пусть , - константы,

тогда .

Условия независимости криволинейного интеграла
от пути интегрирования в односвязной
области на плоскости

Определение односвязности:

Опр. Область D называется односвязной, если для простой замкнутой кривой, являющейся границей области D₁ следует .

Следующие четыре условия – являются условиями эквивалентности:

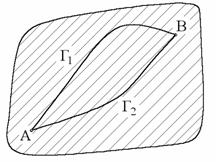
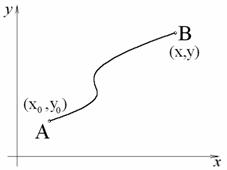
1) (кривые Г₁ и Г₂ имеют одинаковое начало – точку А и одинаковый конец – точку В)

2)справедливо для любой кусочногладкой замкнутой кривой Г.

3) , .

4), в этом случае .

Доказательство:

1)~2)

.

2)~3) , применим формулу Грина:

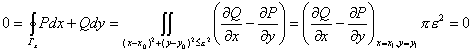,следовательно,

, но

, а при ,следовательно,

.

4)~1) ,это можно представить в виде:, итак,

.

Дифференциальное выражение похоже на выражение полного дифференциала функции
от двух переменных ,которое отождествляется с , если положить .

,докажем, что , следовательно .

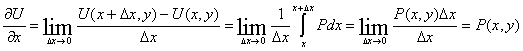,а выражение для примет вид 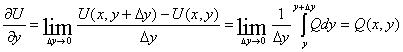, следовательно, является точным дифференциалом.