Лекция 8.

Формула Стокса

Эта формула, как и формула Гаусса-Остроградского, является одной из важнейших в курсе. Для того, чтобы ее вывести, введем понятие ротора векторного поля:

Определение. Назовем ротором величину: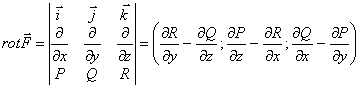

(Существует и другое обозначение ротора: . По существу, ротор является «векторным произведением» оператора Гамильтона на вектор в данной точке пространстве). Ротор является одной из характеристик поля.

Γ+ S	Пусть задана поверхность S, выбрано направление вектора нормали. Считаем, что поверхность гладкая, а контур Γ+ – кусочно-гладкий. Формула Стокса имеет вид:

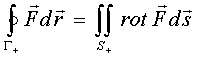
Связь ориентации нормали с направлением обхода можно осуществить при помощи «правила буравчика»: направление движения правого винта при вращении по направлению обхода Γ₊ указывает направление вектора нормали . Другой способ: если смотреть из конца вектора , то обход Γ₊ будет осуществляться против часовой стрелки. Перепишем формулу Стокса в другом виде:

Левая часть – это криволинейный интеграл второго типа, а правая – поверхностный интеграл первого рода.

Формула Стокса доказывается в предположении, что функции P, Q и R – непрерывно дифференцируемы, поверхность, как уже было сказано, гладкая, контур – кусочно-гладкий.

Представим поле в виде суммы: ; ; ; . Доказательство проведем для каждого из полей , и по отдельности.

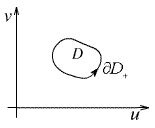
Ротор поля : . Будем считать, что поверхность S задается системой уравнений: 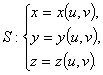Обход контура ∂D₊ осуществляется против часовой стрелки – область D остается слева от контура.

Правая часть формулы: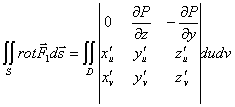

Левая часть - , в пространстве переменных u,v будет иметь вид: . Отсюда по формуле Грина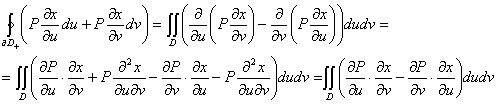

Вычислим производные по u и v. 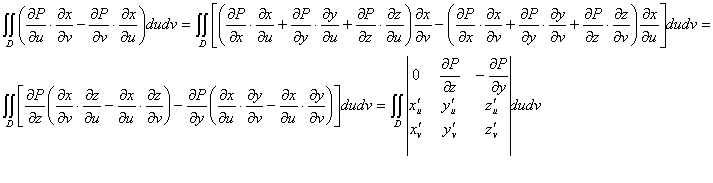Совершенно аналогично выглядит доказательство для полей и .

Формула Грина является частным случаем формулы Стокса. Рассматривается случай плоской поверхности, вектор нормали имеет координаты

Из формулы Грина вытекает следствие о независимости интеграла от пути интегрирования на плоскости. Аналогично можно вывести независимость криволинейного интеграла 2 типа от пути интегрирования в поверхностно-односвязной области в пространстве.

При каких условиях справедливо ?

Для справедливости этого равенства в пространстве должны выполняться следующие условия:

1.

2.

3. (отличие случая пространства от плоскости)

4. Существует такая функция , что . Функцию называют потенциалом данного поля.

В этом случае - разность потенциалов (аналог формулы Ньютона-Лейбница).

Для доказательства нужно воспользоваться формулой Стокса. Так как ротор равен нулю, то интеграл по замкнутой траектории также равен нулю и интеграл не зависит от траектории.

Условие односвязности является существенным. Приведем пример (на плоскости).

Вычислить (интеграл берется по окружности). Попробуем применить формулу Грина: . Вычислим произведение ротора поля на вектор нормали: . Следует ли отсюда, что интеграл по окружности равен нулю? Чтобы проверить это, сделаем параметризацию:

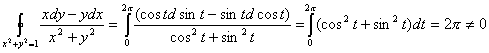
Область должна быть односвязной, т.е. внутри окружности все функции должны быть непрерывны. Но и . Чтобы интегрировать, нужно удалить из рассмотрения точку (0,0), после чего можно применять формулу Грина. Такие же примеры можно привести и для пространства (гравитационное поле с центром в начале координат).